Derivatives as the Rate of Change

\(\frac{dy}{dx} \) is nothing but the rate of change of \(y\), relative to \(x\). If a variable quantity \(y\) is some function of time \(t\) i.e. \(y=f(t),\) then small change in time \(\Delta t\) have a corresponding change \(\Delta y\ in\ y\). Thus the average rate of change \(=\frac{\Delta y}{\Delta t}\)

When limit \(\Delta t \to0\) is applied, the rate of change becomes instantaneous and we get the rate of change with respect to at the instant \(t\), i.e. \(\lim\limits_{\Delta t \to\ 0}\ \frac{\Delta y}{\Delta t}=\ \frac{dy}{dt}\)

\(\frac{dy}{dt}\) is positive if \(y\) increases as \(t\) increase and it is negative if \(y\) decrease as \(t\) increase.

Increasing and Decreasing Function

\(\bullet\)  A function \(f\) is said to be an increasing function in \(]a,\ b[,\ if\ x_1 \lt x_2\ \Rightarrow f(x_1) \le f(x_2),\ \forall\ x_1,\ x_2\ \in]\ a,\ b[.\)

\(\bullet\)  A function \(f\) is said to be a decreasing function in \(]a,\ b[,\ if\ x_1 \lt x_2\ \Rightarrow f(x_1) \ge f(x_2),\ \forall\ x_1,\ x_2\ \in]\ a,\ b[.\)

\(\bullet\)  \(f(x)\) is known as increasing, if \(f'(x) \ge 0\) and decreasing, if \(f'(x) \le 0.\)

\(\bullet\ \ f(x)\) is known as strictly increasing, if \(f'(x) \gt 0\) and strictly decreasing, if \(f'(x) \lt 0\).

\(\bullet\)  Let \(f(x)\) be a function that is continuous in \([a,\ b]\) and differentiable in \((a,\ b)\). Then,

   (i)  \(f(x)\) is an increasing function in \([a,\ b],\text{if}\ \ f'(x) \gt\ 0\ \ \text{in}\ \ (a,\ b).\)

  (ii)  \(f(x)\) is strictly increasing function in \((a,\ b),\text{if}\ \ f'(x) \gt\ 0\ \ \text{in}\ \ (a,\ b).\)

  (iii)  \(f(x)\) is a decreasing function in \([a,\ b],\text{if}\ \ f'(x) \lt\ 0\ \ \text{in}\ \ (a,\ b).\)

  (iv)  \(f(x)\) is a strictly decreasing function in \([a,\ b],\text{if}\ \ f'(x) \lt\ 0\ \ \text{in}\ \ (a,\ b).\) 

Monotonic Function

A function \(f\) is said to be a monotonic in an interval, if it is either increasing or decreasing in that interval.

Results on Monotonic Function

  (i)  If \(f(x)\) is a strictly increasing function on an interval \([a,\ b],\) then \(f^{-1}\) exists and it is also a strictly increasing function.

  (ii)  If \(f(x)\) is strictly increasing function on an interval \([a,\ b]\) such that is continuous, then \(f^{-1}\) is continuous \([f(a),\ f(b)].\)

  (iii)  If \(f(x)\) is continuous on \([a,\ b]\) such that \(f'(c) \ge 0\ [f'(c) \gt0]\) for each \(c\ \in\ (a,\ b),\) then \(f(x)\) is monotonically increasing on \([a,\ b]\)

  (iv)  If \(f(x)\) is continuous on \([a,\ b]\) such that \(f'(c) \le 0\ (f'(c) \lt0)\) for each \(c\ \in\ [a,\ b],\) then \(f(x)\) is monotonically decreasing.

Maxima and Minima of a Function

A function \(f(x)\) is said to attain a maximum at \(x=a,\) if there exists a neighbourhood \((a\ -\delta,\ a\ + \delta),\ x\ \ne a\ \ i.e.\ f(x)\ \lt f(a),\)

\(\forall\ x \in (a\ -\delta,\ a\ + \delta),\ x \ne a\ \cdot\ h \gt 0\)  (very small quantity) 

In such a case \(f(a)\) is said to be the maximum value of \(f(x)\) at \(x=a\).

A function \(f(x)\) is said to attain a minimum at \(x=a,\) if there exists a neighbourhood \((a\ -\delta,\ a\ + \delta)\) such that \( f(x)\ \gt f(a),\ \forall\ x \in (a\ -\delta,\ a\ + \delta),\ x \ne a.\)

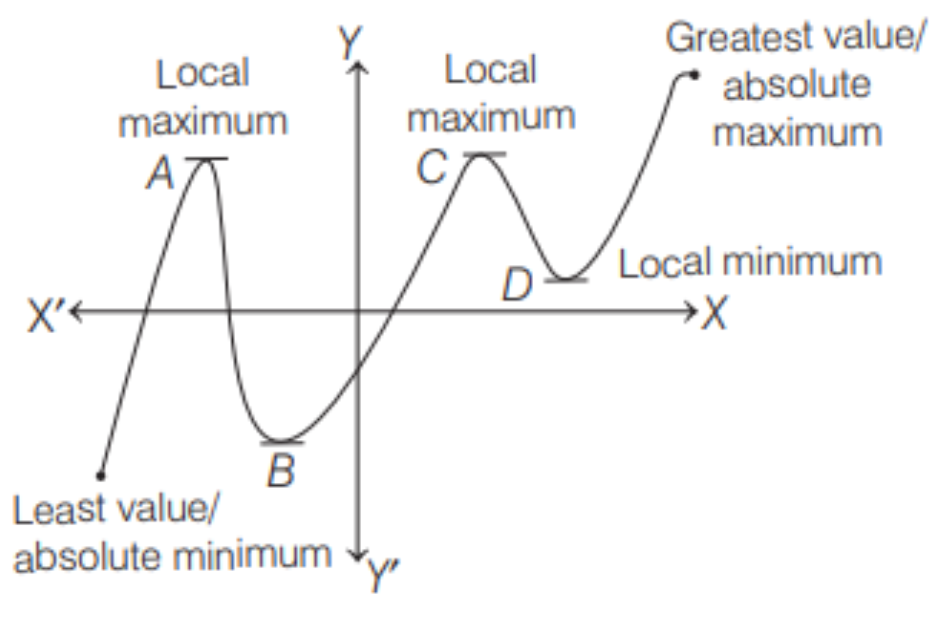
Graph of a continuous function explained local maxima (minima) and absolute maxima (minima). In such a case \(f(a)\) is said to be the minimum value of \(f(x)\) at \(x=a\).

The points at which a function attains either the maximum or the minimum values are known as the extreme points or turning points and both minimum and maximum values of \(f(x)\) are called extreme values. The turning points \(A\ and\ C\) are called local maximum and points \(B\ and\ D\) are called local minimum.

Critical Point

\(\bullet\)  A point \(c\) in the domain of a function \(f\) at which either \(f'(c)=0\) or \(f\) is not differentiable is called a critical point of \(f.\) Note that, if \(f\) is continuous at point \(c\) and \(f'(c)=0,\) then there exists \(h\ \gt 0\) such that \(f\) is differentiable in the interval \((c-h,\ c+h).\)

\(\bullet\)  The converse of above theorem need not be true, that is a point at which the derivative vanishes need not be a point of local maxima or local minima.

Method to Find Local Maxima or Local Minima

First Derivative Test

Let \(f\) be a function defined on an open interval \(I\ and\ F\) be continuous at a critical point \(c\) in \(I.\) Then

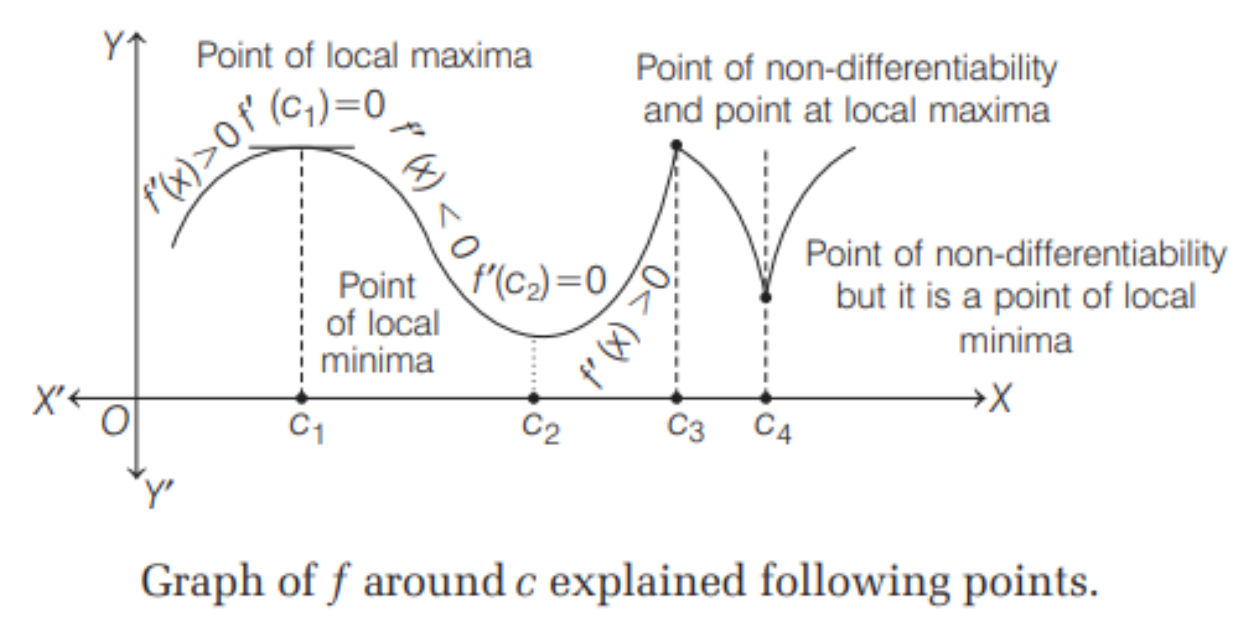
   (i)  If \(f'(x)\) changes sign from positive to negative as \(x\) increases through \(c,\ i.e.\) if \(f'(x) \gt 0\) at every point sufficiently close to and to the left of \(c\) and \(f'(x) \lt 0\) at every point sufficiently close to and to the right of \(c\), then \(c\) is a point of local maxima.

, 

(ii)  If \(f'(x)\) changes sign from negative to positive as \(x\) increases through point \(c\), i.e. if \(f'(x) \lt 0\) at every point sufficiently close to and to the left of \(c\ and\ f'(x) \gt 0\) at every point sufficiently close to and to the right of \(c,\) then \(c\) is a point of local minima.

(iii)  If \(f'(x)\) does not change sign as \(x\) increases through \(c\), then \(c\) is neither a point of local maxima nor a point of local minima. Infact, such a point is called point of inflection.

(iv)  If \(c\) is a point of local maxima of \(f,\) then \(f(c)\) is a local maximum value of \(f\). Similarly, if \(c\) is a point of local minima of \(f\), then \(f(c) \) is a local minimum value of \(f\).

Second or Higher Order Derivative Test

   (i)  Find \(f'(x)\) and equate it to zero. Solve \(f'(x)=0\) let its roots be \(x=a_1,\ a_2,\ ...\)

  (ii)  Find \(f''(x)\) and at \(x=a_1,\)

    (a)  if \(f''(a_1)\) is positive, then \(f(x)\) is minimum at \(x=a_1.\)

    (b)  if \(f''(a_1)\) is negative, then \(f(x)\) is maximum at \(x=a_1.\)

  (iii)   (a)  If at \(x=a_1,\ f''(a_1)=0,\) then find \(f'''(x).\) If \(f'''(a_1)\ \ne0,\) then \(f(x)\) is neither maximum nor minimum at \(x=a.\)

          (b)  If \(f'''(a_1)=0,\) then find \(f^{iv}(x).\)

          (c)  If \(f^{iv}(x)\) is positive \(\)(minimum value) and \(f^{iv}(x)\) is negative (maximum value).

(iv)  If at \(x=a_1,\ f^{iv}(a_1)=0, \) then find \(f^v(x)\) and proceed similarly.

Point of Inflection

At point of inflection

   (i)  It is not necessary that 1st derivative is zero.

   (ii)  2nd derivative must be zero or 2nd derivative changes sign in the neighbourhood of point of inflection.

nth Derivative Test

Let \(f\) be a differentiable function on an interval \(I\ and\ a\) be an interior point of \(I\) such that

   (i)  \(f'(a)=\ f''(a)\ = f'''(a)=\ ...=\ f^{n-1}\ (a)=0\) and

   (ii)  \(f^n(a)\) exists and is non-zero.

Important Results

\(\bullet\)  If \(n\) is even and \(f^n(a) \lt 0 \Rightarrow x=a\) is a point of local maximum.

\(\bullet\)  If \(n\) is even and \(f^n(a) \gt 0 \Rightarrow x=a\) is a point of local minimum.

\(\bullet\) If \(n\) is odd \(\Rightarrow x=a\) is a point of neither local maximum nor a point of local minimum.

\(\bullet\)  The function \(f(x)=\frac{ax\ +\ b}{cx\ +\ d}\) has no local maximum or minimum regardless of values of \(a,\ b,\ c\ and\ d\).

\(\bullet\)  The function \(f(\theta)=\ \sin^m\ \theta \cdot\ \cos ^n\ \theta\) attains maximum values at \(\theta= \tan^{-1}\Big(\sqrt{\frac{m}{n}}\Big).\)

\(\bullet\)  If \(AB\) is diameter of circle and \(C\) is any point on the circumference, then area of the \(\Delta\ ABC\) will be maximum, if triangle is isosceles.

Concept of Global Maximum / Minimum

\(\bullet\)  Let \(y=f(x)\) be a given function with domain \(D\) and \([a,\ b]\ \subseteq\ D,\) then global maximum / minimum of \(f(x)\ in\ [a,\ b]\) is basically the greatest / least value of \(f(x)\ in\ [a,\ b]\).

\(\bullet\)  Global maxima / minima in \( [a,\ b]\) or at end points of the interval.

Global Maximum / Minimum in [a, b]

In order to find the global maximum and minimum of \(f(x)\) in \([a,\ b]\).

   Step I  Find out all critical points of \(f(x)\) in \([a,\ b]\) [i.e. all points at which \(f'(x)=0\) ] and let these points are \(c_1,\ c_2,\ ...,\ c_n.\)

   Step II  Find the value of \(f(c_1),\ f(c_2),\ ...,\ f(c_n)\) and also at the end points of domain i.e. \(f(a)\ and \ f(b).\)

   Step III  Find \(M_1\ \to\) Global maxima or greatest value

                 and \(M_1\ \to\) Global minima or least value.

                 Where, \(M_1=\max\ \{f(a),\ f(c_1),\ f(c_2),\ ...,\ f(c_n),\ f(b)\}\)

                and \(M_2=\min\ \{f(a),\ f(c_1),\ f(c_2),\ ...,\ f(c_n),\ f(b)\}\)

Some Important Results On Maxima and Minima

(i)  Maxima and minima occur alternatively i.e. between two maxima there is one minimum and vice-versa.

(ii)  If \(f(x)\ \to\ \infty\) as \(x\ \to\ a\ or\ b\) and \(f'(x)=0\) only for one value of \(x\) (say c) between \(a\ and\ b,\) then \(f(c)\) is necessarily the minimum and the least value.

(iii)  If \(f(x)\ \to\ -\infty\ \ as\ \ x\ \to\ a\ or\ b\), then \(f(c)\) is necessarily the maximum and the greatest value.

(iv)  The stationary points are the points of the domain, where \(f'(x)=0.\)