Parametric Differentiation Rule
(ix) If \(x=\phi\ (t)\ and\ y= \Psi\ (t),\) where \(t\) parameter, then \(\frac{dy}{dx}=\ \frac{dy/dt}{dx/dt}\) [Parametric differentiation rule]
(x) If \(u=f(x)\ and\ v= g(x),\) the differentiation of \(u\) with respect to \(v\) is \(\frac{du}{dv}=\frac{\big(\frac{du}{dx}\big)}{\big(\frac{dv}{dx}\big)}.\) [Differentiation of a w. r. t another function]


Differentiation Using Substitution-I
Differentiation Using Substitution
In order to find differential coefficients of complicated expressions, some substitution are very helpful, which are listed below



Second Order Derivative
Second Order Derivative
If \(y=f(x),\ then\ \frac{d}{dx}\ \Big(\frac{dy}{dx}\Big)\) is called the second order derivative of \(y\) w.r.t \(x\). It is denoted by \(\frac{d^2 y}{dx^2}\ or\ f''(x)\ or\ y''\ or\ y_2.\)
Differentiate of Determinant
If \(\begin{vmatrix}p&q&r\\u&v&w\\l&m&n\end{vmatrix}\)
then
\(\frac{dy}{dx}=\begin{vmatrix}\frac{dp}{dx}&\frac{dq}{dx}&\frac{dr}{dx}\\u&v&w\\l&m&n\end{vmatrix}\ +\ \begin{vmatrix}p&q&r\\\frac{du}{dx}&\frac{dv}{dx}&\frac{dw}{dx}\\l&m&n\end{vmatrix}\ +\ \begin{vmatrix}p&q&r\\u&v&w\\\frac{dl}{dx}&\frac{dm}{dx}&\frac{dn}{dx}\end{vmatrix}\)


Continuity
Continuity
If the graph of a function has no break (or gap), then it is continuous. A function which is not continuous is called a discontinuous function. e.g. \(x^2\) and \(e^x\) are continuous while \(\frac{1}{x}\) and [x], where \([\cdot]\) denotes the greatest integer function, are discontinuous.


Derivative (Differential Coefficient)
Derivative (Differential Coefficient)
The rate of change of a quantity \(y\) with respect to another quantity \(x\) is called the derivative or differential coefficient of \(y\) with respect to \(x\). The process of finding derivative of a function called differentiation.
Geometrical Meaning of Derivative at a Point
Geometrically derivative of a function at a point \(x=c\) is the slope of the tangent to the curve \(y=f(x)\) at the point \(P\ \{c,\ f(c)\}.\)
Slope of tangent at \(P= \lim\limits_{x \to c}\ \frac{f(x)\ -\ f(c)}{x\ -\ c}=\ \Big\{\frac{df(x)}{dx}\Big\}_{x=c}\ \ or\ \ f'(c).\)


Continuity Of A Function At A Point
Continuity of a Function at a Point
A function \(f(x)\) is said to be continuous at a point \(x=a\) of its domain if and only if it satisfies the following conditions.
(i) \(f(a)\) exists, where ( \('a'\) lies in the domain of \(f\) )
(ii) \(\lim\limits_{x \to a}\ f(x)\) exist, i.e. \(\lim\limits_{x \to a^-}\ f(x)=\lim\limits_{x \to a^+}\ f(x)\) or LHL = RHL
(iii) \(\lim\limits_{x \to a}\ f(x)= f(a),\ f(x)\) is said to be
left continuous at \(x=a, \text{if} \ \lim\limits_{x \to a^-}\ f(x)=f(a)\)
right continuous at \(x=a, \text{if} \ \lim\limits_{x \to a^+}\ f(x)=f(a)\)


Methods Of Differentiation-II
(vi) \(\frac{d}{dx}\ (f\ \{g(x)\})= f'(g(x))\ \cdot g'(x)\)
(vii) If given function cannot be expressed in the form \(y=f(x)\) but can be expressed in the form \(f(x,\ y)=0,\) then to find derivatives of each term of \(f(x,\ y)=0\) w.r.t \(x\) [differentiation of implicit function]
(vi) If \(y \) is the product or the quotient of a number of complicated functions or if it is of the form \((f(x))^{g(x)},\) then the derivative of \(y\) can be found by first taking log on both sides and then differentiating it. [logarithmic differentiation rule]
When \(y=(f(x))^{g(x)},\ then\ \frac{dy}{dx}=\ (f(x))^{g(x)}\ \Big[\frac{g(x)}{f(x)}\ \cdot f'(x)\ +\ \log f(x) \cdot\ g'(x)\Big]\)


Methods Of Differentiation
Methods of Differentiation
(i) If \(y=f(x)\ \pm\ g(x),\ then\ \frac{dy}{dx}=\ \frac{d}{dx}\ \{f(x)\ \pm\ g(x)\}= f'(x)\ \pm\ g'(x)\)
(ii) If \(y=c\ \cdot f(x),\) where \(c\) is any constant, then \(\frac{dy}{dx}=\frac{d}{dx}\ (c\ \cdot f(x))= c\ \cdot f'(x).\) [Scalar multiple rule]
(iii) If \(y=f(x)\ \cdot g(x), \ then\ \frac{dy}{dx}=\ \frac{d}{dx}\ \{f(x)\ \cdot g(x)\}=\ f(x)\ \cdot g'(x)\ +\ g(x)\ \cdot f'(x)\) [Product rule]
(iv) If \(y=\frac{f(x)}{g(x)},\ then\ \frac{dy}{dx}=\ \frac{d}{dx}\ \Big\{\frac{f(x)}{g(x)}\Big\}= \frac{g(x)\ \cdot f'(x)\ -\ f(x)\ \cdot g'(x)}{\{g(x)\}^2}\ \ g(x) \ne 0\)
(v) If \(y= f(u)\ and\ u= g(x),\ then\ \frac{dy}{dx}= \frac{df}{du} \cdot \frac{du}{dx}= f'(u)\ \cdot g'(x)\) [Chain rule]
This rule can be extended as follows, If \(y= f(u),\ u= g(v)\ and\ v=h(x), \ then\ \frac{dy}{dx}=\frac{df}{du} \cdot \frac{du}{dv} \cdot \frac{dv}{dx}\)


Derivative Of Standard Functions-II
\(\bullet\ \ \frac{d}{dx}\ (\sin^{-1}\ x)= \frac{1}{\sqrt{1-x^2}},\ \ for\ \ -1\ \lt\ x\ \lt\ 1\\ \bullet\ \ \frac{d}{dx}\ (\cos^{-1}\ x)= -\frac{1}{\sqrt{1-x^2}},\ \ for\ \ -1\ \lt\ x\ \lt\ 1\\ \bullet\ \ \frac{d}{dx}\ (\sec^{-1}\ x)= \frac{1}{|x|\ \sqrt{x^2\ -\ 1}},\ \ for\ \ |x|\ \gt\ 1\\ \bullet\ \ \frac{d}{dx}\ (\text{cosec}^{-1}\ x)= -\frac{1}{|x|\ \sqrt{x^2\ -\ 1}},\ \ for\ \ |x|\ \gt\ 1\\ \bullet\ \ \frac{d}{dx}\ (\tan^{-1}\ x)= \frac{1}{1\ +\ x^2},\ for\ \ x \in R\\ \bullet\ \ \frac{d}{dx}\ (\cot^{-1}\ x)= -\frac{1}{1\ +\ x^2},\ for\ \ x \in R\)


Results On Differentiability
Results on Differentiability
(i) Every polynomial, constant and exponential function is differentiable at each \(x \in R.\)
(ii) The logarithmic, trigonometric and inverse trigonometric function are differentiable in their domain.
(iii) The sum, difference, product and quotient of two differentiable functions is differentiable.
(iv) Every differentiable function is continuous but converse may or may not be true.


Differentiability
Differentiability
The function \(f(x)\) is differentiable at a point \(P\) iff there exists a unique tangent at point \(P\). In other words, \(f(x)\) is differentiable at a point \(P\) iff the curve does not have \(P\) as a corner point, i.e. the function is not differentiable at those points where graph of the function has holes or sharp edges. Let us consider the function \(f(x)=\ |x\ -\ 1|.\) It is not differentiable at \(x=1.\) Since, \(f(x)\) has sharp edge at \(x=1\).
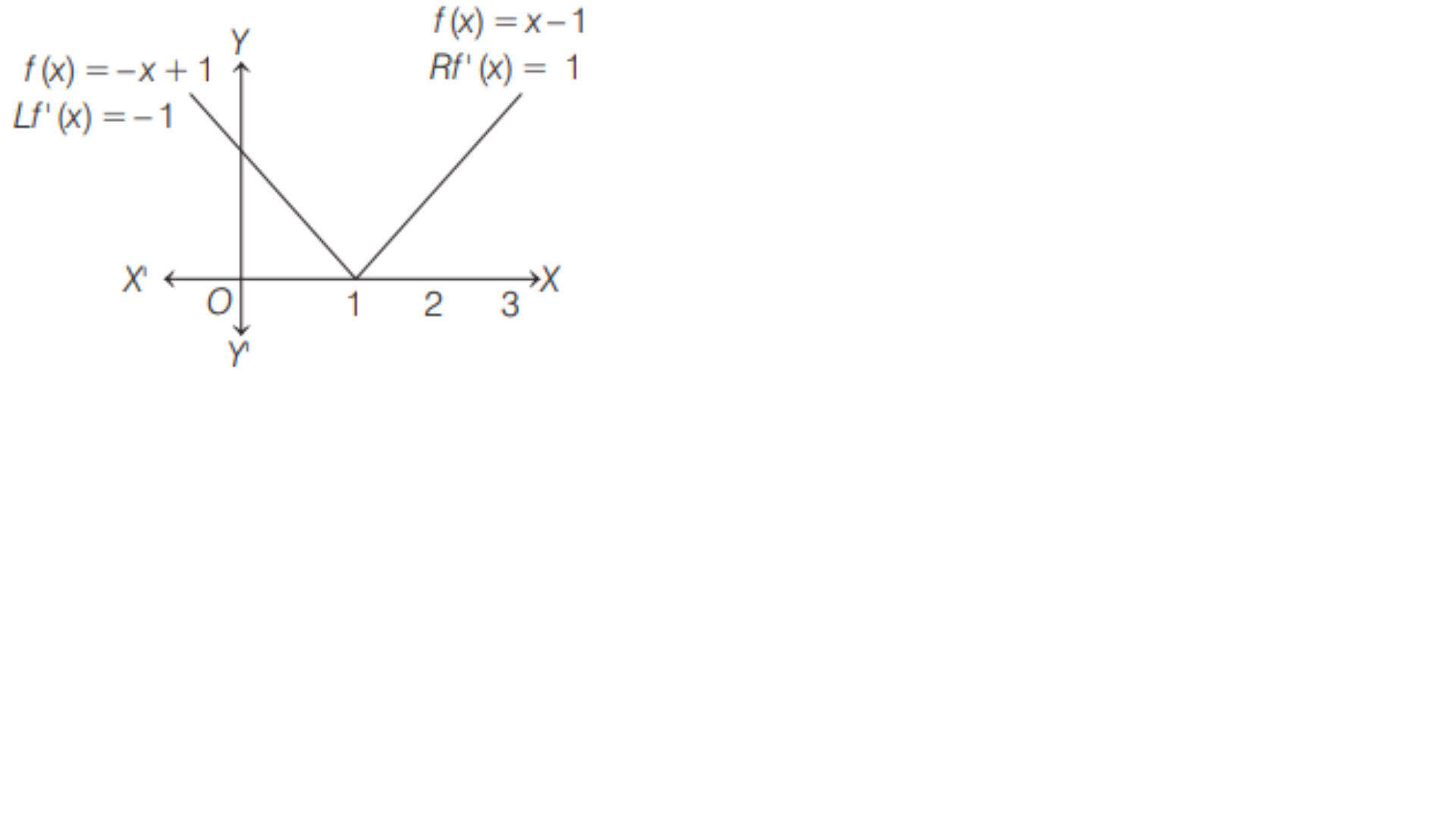 (graph of \(f(x)\) describe differentiability)
(graph of \(f(x)\) describe differentiability)


Results On Continuous Functions
Results on Continuous Functions
(i) Sum, difference product and quotient of two continuous functions are always a continuous functions. However, \(r(x)= \frac{f(x)}{g(x)}\) is continuous at \(x=a\) only if \(g(a)\ne 0.\)
(ii) Every polynomial is continuous at each point of real line.
(iii) Every rational function is continuous at each point where its denominator is different from zero.
(iv) Logarithmic functions, exponential functions, trigonometric functions, inverse circular functions and modulus function are continuous in their domain.
(v) \([x]\) is discontinuous when \(x\) is an integer.


Derivative Of Standard Functions-I
Derivative of Some Standard Functions
\(\bullet\ \ \frac{d}{dx}\ (constant)\ = 0\\ \bullet\ \ \frac{d}{dx}\ (\sqrt x)=\ \frac{1}{2\sqrt x}\\ \bullet\ \ \frac{d}{dx}\ (\sin x)= \ \cos x\\ \bullet\ \ \frac{d}{dx}\ (\tan x)= \sec^2\ x\\ \bullet\ \ \frac{d}{dx}\ (\cot x)=\ -\text{cosec}^2\ x\\ \bullet\ \ \frac{d}{dx}\ (\log x)=\frac{1}{x},\ for\ \ x \gt 0\\ \bullet\ \ \frac{d}{dx}\ (a^x)\ =a^x\ \log\ a,\ for\ \ a \gt 0\)
\(\bullet\ \ \frac{d}{dx}\ x^n= nx^{n\ -\ 1}\\ \bullet\ \ \frac{d}{dx}\ \Big(\frac{1}{x^n}\Big)=\ -\frac{n}{x^{n\ +\ 1}}\\ \bullet\ \ \frac{d}{dx}\ (\cos x)=\ -\ \sin x\\ \bullet\ \ \frac{d}{dx}\ (\sec x)= \sec x\ \tan x\\ \bullet\ \ \frac{d}{dx}\ (\text{cosec}\ x)=\ - \text{cosec}\ x\ \cot\ x\\ \bullet\ \ \frac{d}{dx}\ (e^x)=e^x\\ \bullet\ \ \frac{d}{dx}\ (\log_a\ x)=\frac{1}{x\ \log\ a},\ \ for\ \ x \gt 0,\ a \gt 0,\ a \ne 1\)


Differentiability Of A Function At A Point
Differentiability of a Function at a Point
A function \(f\) is said to be differentiable at \(x=c,\) if left hand and right hand derivatives at \(c\) exist and are equal.
\(\bullet\) Right hand derivative of \(f(x)\ \ at\ \ x=a\) denoted by \(f'(a\ +\ 0)\ \ or\ \ f'(a^+)\ \ is\ \ \lim\limits_{h \to 0}\ \frac{f(a\ +\ h)\ -\ f(a)}{h}.\)
\(\bullet\) Left hand derivative of \(f(x)\ \ at\ \ x=a\) denoted by \(f'(a\ -\ 0)\ \ or\ \ f'(a^-)\ \ is\ \ \lim\limits_{h \to 0}\ \frac{f(a\ -\ h)\ -\ f(a)}{-h}.\)
\(\bullet\) Thus, \(f\) is said to be differentiable at \(x=a,\) if \(f'(a\ +\ 0)=f'(a\ -\ 0)= \text{finite}.\)
\(\bullet\) The common limit is called the derivative of \(f(x)\ \ at\ \ x=a\) denoted by \(f'(a).\ i.e.\ f'(a)=\lim\limits_{x \to a}\ \frac{f(a\ +\ h)\ -\ f(a)}{h}.\)


 beeTokens
beeTokens 



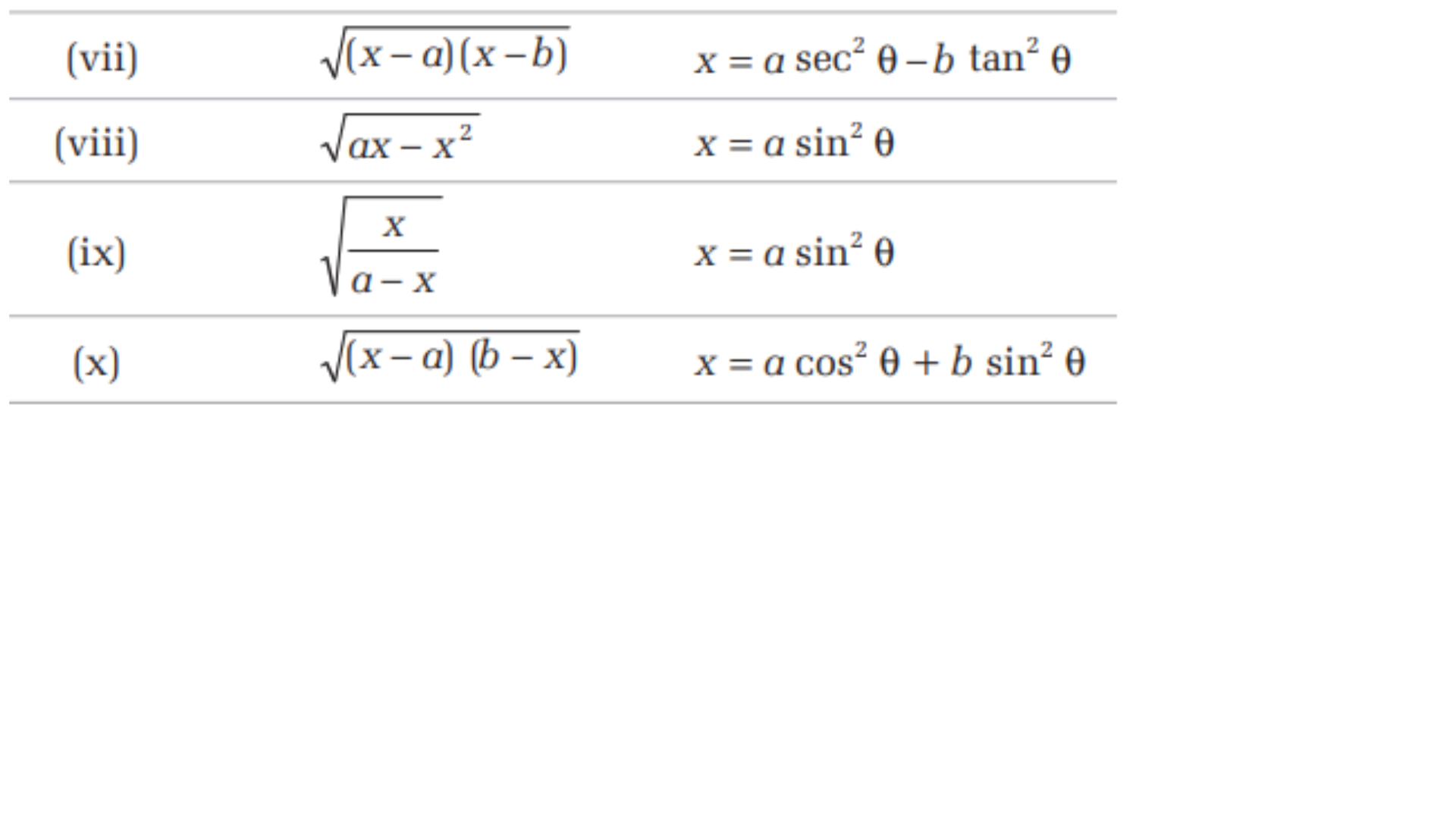 Usually this is done in case of inverse of trigonometric functions.
Usually this is done in case of inverse of trigonometric functions.