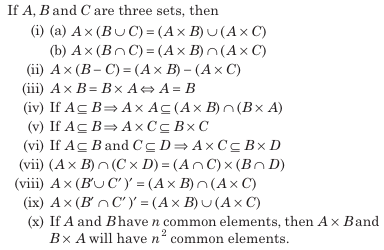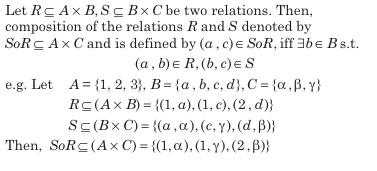Ordered Pair & Cartesian Product
In Mathematics we come across many relations such as number m is less than number n, line l is parallel to line m. In all these, a relation involves pairs of objects in certain order. A special type of relation called function. Concept of function plays very important role in Mathematics, since it captures the idea of a mathematically precise correspondence between one quantity with the other.
Ordered Pair
Two elements a and b listed in a specific order form an ordered pair, denoted by (a, b). In an ordered pair (a, b) ; a is regarded as the first element and b is the second element.
It is evident from the definition that
(i) \((a, b) \neq(b, a)\)
(ii) \((a, b)=(c, d) iff a=c, b=d\)
Equality of Ordered Pair
Two ordered pairs \((a_1, b_1 ) and ( a_2, b_2 )\) are equal iff
\(
\begin{array}{ll}
& a_1=a_2 \text { and } b_1=b_2 \\
\text { i.e., } & \left(a_1, b_1\right)=\left(a_2, b_2\right) \\
\Rightarrow & a_1=a_2 \text { and } b_1=b_2
\end{array}
\)
Thus, it is evident from the definition that \((1,2) \neq(2,1) and (1,1) \neq(2,2)\)
Cartesian Product
Let A and B be two non-empty sets. The cartesian product of A and B is denoted by \(A \times B\) and is defined as the set of all ordered pairs ( a, b ), where \(a \in A and b \in B\)
Symbolically, \(A \times B=\{(a, b): a \in A and b \in B\}\)


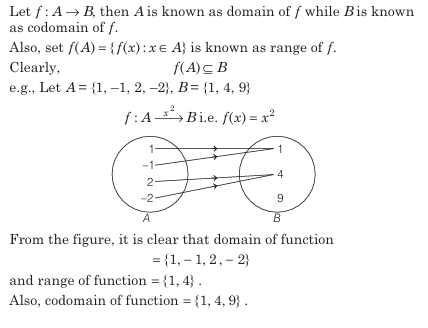
Functions Or Mappings
Let A and B be two non-empty sets. Then, a function f from set A to B is a rule which associates elements of set A to elements of B such that all elements of set A are associated to elements of set B in unique way.
If f associates \(x \in A to y \in B,\) then we say that y is the image of the element x and denote it by $(x) and write as y=f(x). The element x is called the pre-image or inverse image in $B$.
A function is denoted by \(f: A \rightarrow B or A \xrightarrow{f} B\)
Note
- There may exist some elements in set B which are not the images of any element in set A
- To each and every independent element in A there corresponds one and only one image in B
- Every function is a relation but every relation may or may not be a function.
- The number of functions from a finite set A into finite set \(B=[n(B)]^{[n(A)]}\)


Polynomial Function
Polynomial function: A real valued function f : R → R defined by f(x) = a0 + a1x + a2x2+…+ anxn, where n ∈ N and a0, a1, a2,…….. an ∈ R for each x ∈ R, is called polynomial function.
Rational function: These are the real function of type f(x)g(x), where f(x)and g(x)are polynomial functions of x defined in a domain, where g(x) ≠ 0.


The Modulus Function
The modulus function: The real function f : R → R defined by f(x) = |x|
or
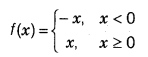
for all values of x ∈ R is called the modulus function.
Domaim of f = R
Range of f = R+ U {0} i.e. [0, ∞)


Signum Function
Signum function: The real function f : R → R defined
by f(x) = |x|x, x ≠ 0 and 0, if x = 0
or
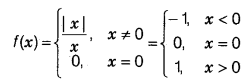
is called the signum function.
Domain of f = R; Range of f = {-1, 0, 1}


Fractional Part Function
Greatest integer function: The real function f : R → R defined by f (x) = {x}, x ∈ R assumes that the values of the greatest integer less than or equal to x, is called the greatest integer function.
Domain of f = R; Range of f = Integer
Fractional part function: The real function f : R → R defined by f(x) = {x}, x ∈ R is called the fractional part function.
f(x) = {x} = x – [x] for all x ∈R
Domain of f = R; Range of f = [0, 1)


Algebra Of Real Functions
Algebra of Real Functions
Addition of two real functions: Let f : X → R and g : X → R be any two real functions, where X ∈ R. Then, we define (f + g) : X → R by
{f + g) (x) = f(x) + g(x), for all x ∈ X.
Subtraction of a real function from another: Let f : X → R and g : X → R be any two real functions, where X ⊆ R. Then, we define (f – g) : X → R by (f – g) (x) = f (x) – g(x), for all x ∈ X.


Multiplication By A Scalar
Multiplication by a scalar: Let f : X → R be a real function and K be any scalar belonging to R. Then, the product of Kf is function from X to R defined by (Kf)(x) = Kf(x) for all x ∈ X.
Multiplication of two real functions: Let f : X → R and g : X → R be any two real functions, where X ⊆ R. Then, product of these two functions i.e. f.g : X → R is defined by (fg) x = f(x) . g(x) ∀ x ∈ X.


Quotient Of Two Real Functions
quotient of two real functions: Let f and g be two real functions defined from X → R. The quotient of f by g denoted by fg is a function defined from X → R as



 beeTokens
beeTokens