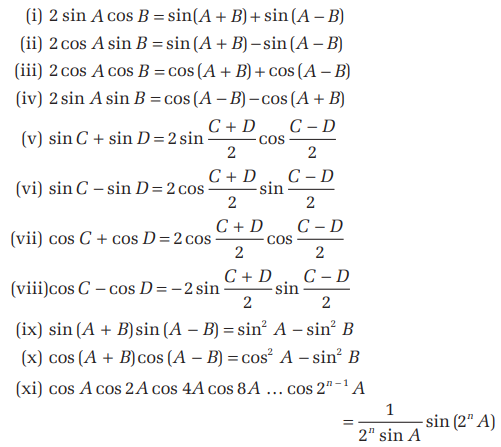Facts Related to \(\cos x\)
(a) Domain \(=R\)
(b) Range \(=[-1,1]\)
(c) Period \(=2 \pi\)
(d) Graph of \(\cos x\) is continuous for all real values of \( x\)

Tips to Remember:

• 15° and 75° are symmetric around 45°.

• 30°, 45°, 60° are standard — you must master them!

• Values at 18°, 36°, 54°, 72° involve √5, related to pentagons (Golden Ratio).

• 22.5° and 67.5° involve √2.

• At 90°: sin = 1, cos = 0, tan = ∞.

(i) \(\sin (A+B)=\sin A \cos B+\cos A \sin B\)
(ii) \(\sin (A-B)=\sin A \cos B-\cos A \sin B\)
(iii) \(\cos (A+B)=\cos A \cos B-\sin A \sin B\)
(iv) \(\cos (A-B)=\cos A \cos B+\sin A \sin B\)
(v) \(\tan (A+B)=\frac{\tan A+\tan B}{1-\tan A \tan B}\)
(vi) \(\tan (A-B)=\frac{\tan A-\tan B}{1+\tan A \tan B}\)
(vii) \( \cot (A+B)=\frac{\cot A \cot B-1}{\cot A+\cot B}\)
(viii) \(\cot (A-B)=\frac{\cot A \cot B+1}{\cot B-\cot A}\)(

 \( \begin{aligned} \sin (A-B) & =\sin ^2 A-\sin ^2 B \\ & =\cos ^2 B-\cos ^2 A \end{aligned} \)

\( \begin{aligned} \cos (A+B) \cos (A-B) & =\cos ^2 A-\sin ^2 B \\ & =\cos ^2 B-\sin ^2 A \end{aligned} \)

 \( \begin{aligned} \sin (A+B+C)= & \sin A \cos B \cos C+\cos A \sin B \cos C \\ & +\cos A \cos B \sin C-\sin A \sin B \sin C \end{aligned} \)

  \( \begin{aligned} \cos (A+B+C)= & \cos A \cos B \cos C-\sin A \sin B \cos C \\ & -\sin A \cos B \sin C-\cos A \sin B \sin C \end{aligned} \)

(i) \(2 \sin A \cos B=\sin (A+B)+\sin (A-B)\)
(ii) \(2 \cos A \sin B=\sin (A+B)-\sin (A-B)\)
(iii) \(2 \cos A \cos B=\cos (A+B)+\cos (A-B)\)
(iv) \(2 \sin A \sin B=\cos (A-B)-\cos (A+B)\)

(i)\( \sin 2 \theta=2 \sin \theta \cos \theta=\frac{2 \tan \theta}{1+\tan ^2 \theta}\)
(ii) \(\cos 2 \theta=\cos ^2 \theta-\sin ^2 \theta=1-2 \sin ^2 \theta\)
= \(2 \cos ^2 \theta-1=\frac{1-\tan ^2 \theta}{1+\tan ^2 \theta} \)
(iii) \(\cos ^2 \theta=\frac{1}{2}(1+\cos 2 \theta), \sin ^2 \theta=\frac{1}{2}(1-\cos 2 \theta)\)
(iv) \(\tan 2 \theta=\frac{2 \tan \theta}{1-\tan ^2 \theta}\)
(v) \(\cot 2 \theta=\frac{\cot ^2 \theta-1}{2 \cot \theta}\)
(vi) \(\sin 3 \theta=3 \sin \theta-4 \sin ^3 \theta\)
(vii) \(\cos 3 \theta=4 \cos ^3 \theta-3 \cos \theta\)
(viii) \( \tan 3 \theta=\frac{3 \tan \theta-\tan ^3 \theta}{1-3 \tan ^2 \theta}\)
(ix) \( \begin{aligned} \cot 3 \theta & =\frac{\cot ^3 \theta-3 \cot \theta}{3 \cot ^2 \theta-1} \\ & =\frac{3 \cot \theta-\cot ^3 \theta}{1-3 \cot ^2 \theta} \end{aligned} \)

(i) \( \sin \theta=2 \sin \frac{1}{2} \theta \cos \frac{1}{2} \theta=\frac{2 \tan \frac{1}{2} \theta}{1+\tan ^2 \frac{1}{2} \theta}\)

(ii) \( \begin{aligned} \cos \theta=\cos ^2 \frac{1}{2} \theta-\sin ^2 \frac{1}{2} \theta & =1-2 \sin ^2 \frac{1}{2} \theta \\ =2 \cos ^2 \frac{1}{2} \theta-1 & =\frac{1-\tan ^2 \frac{1}{2} \theta}{1+\tan ^2 \frac{1}{2} \theta} \end{aligned} \)

(iii) \( \tan \theta=\frac{2 \tan \frac{1}{2} \theta}{1-\tan ^2 \frac{1}{2} \theta}\)
(iv) \(\cot \theta=\frac{\cot ^2 \frac{1}{2} \theta-1}{2 \cot \frac{1}{2} \theta}\)

Note  \( \begin{aligned} & \cdot 1-\cos A=2 \sin ^2 \frac{A}{2} \quad \cdot 1+\cos A=2 \cos ^2 \frac{A}{2} \\ & \text { - } \sin (\alpha)+\sin (\alpha+\beta)+\sin (\alpha+2 \beta)+\ldots+\sin [\alpha+(n-1) \beta] \\ & \\ & =\frac{\sin \left\{\alpha+(n-1)\left(\frac{\beta}{2}\right)\right\} \sin \left(\frac{n \beta}{2}\right)}{\sin \left(\frac{\beta}{2}\right)} \\ & =\frac{\cos (\alpha)+\cos (\alpha+\beta)+\cos (\alpha+2 \beta)+\ldots+\cos [\alpha+(n-1) \beta]}{\sin \frac{\beta}{2}} \end{aligned} \)

An equation involving one or more trigonometrical ratios of unknown angle is called a trigonometric equation. e.g. \(\cos ^2 \theta-\sin \theta=\frac{1}{2}\\\tan m \theta=\cot n \theta\) etc., are trigonometric equations.

Solutions of a Trigonometric Equation
A value of the unknown angle which satisfies the given equation, is called a solution of the equation.
The trigonometric equation may have infinite number of solutions and can be classified as

Principal Solution
The least value of unknown angle which satisfies the given equation, is called a principal solution of trigonometric equation.
General Solution
The solution consisting of all possible solutions of a trigonometric equation is called its general solution.

Note A function $f(x)$ is said to be a periodic function, if a least positive real number \(T\) is such that \(f(x+T)=f(x)\), then  \(T\)  is known as period of function \(f(x)\)

Maximum and Minimum (Greatest and Least) Value of  \(a \sin \theta+b \cos \theta\)
Let  \(a=r \cos \alpha \\ b=r \sin \alpha\)
\( \begin{aligned} \therefore a \sin \theta+b \cos \theta & =r(\cos \alpha \sin \theta+\sin \alpha \cos \theta) \\ & =r \sin (\theta+\alpha) \end{aligned} \)
where, \(r=\sqrt{a^2+b^2}\\\alpha=\tan ^{-1}\left(\frac{b}{a}\right)\)
 Maximum and minimum values of \( \sin (\theta+\alpha)\) are 1 and -1 respectively. Therefore,
(i) Maximum value of \(a \sin \theta+b \cos \theta=\sqrt{a^2+b^2}\)
(ii) Minimum value of  \(a \sin \theta+b \cos \theta=-\sqrt{a^2+b^2}\)

Facts Related to \(\tan x\)
(a) Domain \(=R-(2 n+1) \frac{\pi}{2}, n \in I\)
(b) Range \(=(-\infty, \infty)\)
(c) Period \( =\pi\)
(d) Graph of is an odd integer.

Let\( X^{\prime} O X\)and \(Y O Y^{\prime}\) be the coordinate axes. Taking \(O\) as the centre and a unit radius, draw a circle, cutting the coordinate axes at\( A, B, A^{\prime} and B^{\prime}\), as shown in the figure.

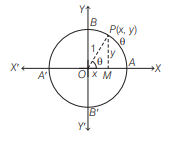
Let \(\angle A O P=\theta\)
\( \left[\because \angle A O P=\frac{\operatorname{arc} A P}{\operatorname{radius} O P}=\frac{\theta}{1}=\theta^c, \text { using } \theta=\frac{l}{r}\right] \)Now, the six trigonometric functions may be defined as under
(i) \(\cos \theta=\frac{O M}{O P}=x\)
(ii) \(\sin \theta=\frac{P M}{O P}=y\)
(iii) \(\sec \theta=\frac{O P}{O M}=\frac{1}{x}, x \neq 0\)
(iv) \(\operatorname{cosec} \theta=\frac{O P}{P M}=\frac{1}{y}, y \neq 0\) 
(v) \( \tan \theta=\frac{P M}{O M}=\frac{y}{x}, x \neq 0\)
(vi) \( \cot \theta=\frac{O M}{P M}=\frac{x}{y}, y \neq 0 \)

Facts Related to \(\sin x\)
(a) Domain \(=R\)
(b) Range \(=[-1,1]\)
(c) Period \( =2 \pi\)
(d) Graph of \(\sin x\) is continuous for all real values of \(x\)