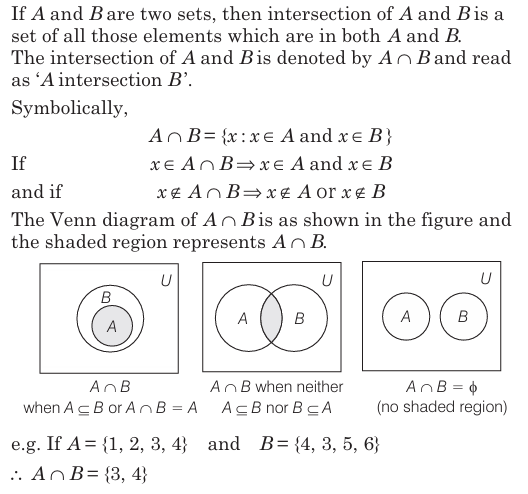
Power Set
Let A be a non-empty set, then collection of all possible subsets of set A is known as power set. It is denoted by \(P(A)\).
e.g. Suppose \( A=\{1,2,3\}\)
\(
\therefore P(A)=\{\phi,\{1\},\{2\},\{3\},\{1,2\},\{2,3\},\{3,1\},\{1,2,3\}\} .
\)
(a) \(A \in P(A)\)
(b) \(\{A\} \notin P(A)\)
Properties of Power Set
(i) Each element of a power set is a set.
(ii) If \(A \subseteq B, then P(A) \subseteq P(B)\)
(iii) Power set of any set is always non-empty.
(iv) If set A has n elements, then \(P(A) has 2^n\) elements.
(v) \(P(A) \cap P(B)=P(A \cap B)\)
(vi) \( P(A) \cup(B) \subseteq P(A \cup B)\)
(vii) \(P(A \cup B) \neq P(A) \cup P(B)\)


Sets And Their Representation
Sets
In Mathematics, a set is a collection of well-defined distinct object or elements. The elements that make up a set can be any kind of things : people letters of alphabet, numbers, geometrical shape, variables or even other sets.
Generally, sets are denoted by capital letters \(A, B, C, \ldots\) and its elements are denoted by small letters \(a, b, c, \ldots\)
Let A is a non-empty set. If x is an element of A, then we write ' \(x \in A\) ' and read as ' x is an element of A ' or ' x belongs to A '. If x is not an element of A, then we write ' \(x \notin A\) ' and read as x is not an element of A ' or ' x does not belong to A '.
e.g. \(A=\) Set of all vowels in English alphabets.
In this set a, e, i, o and u are members.
Representation of Sets
We can use the following two methods to represent a set.
(i) Listing Method In this method, elements are listed and put within a braces \{ \} and separated by commas.
This method is also known as Tabular method or Roster method. e.g. $\quad A= Set of all prime numbers less than \(11=\{2,3,5,7\}\)
(ii) Set Builder Method In this method, instead of listing all elements of a set, we list the property or properties satisfied by the elements of set and write it as
\( A=\{x: P(x)\} \text { or }\{x \mid P(x)\} \)
It is read as A is the set of all elements x such that x has the property P(x).' The symbol '\( \because\) ' or ' \(\mid\) ' stands for such that.
This method is also known as Rule method or Property method. e.g. The set \(A=\{1,2,3,4,5,6,7,8\}\) is written in set builder form
\( A=\{x: x \in N \text { and } x \leq 8\} \)


Different Types Of Sets-1
(i) Empty (Void/Null) Set
A set which has no element, is called an empty set. It is denoted by \(\phi\) or \{\}.
e.g. A= Set of all odd numbers divisible by 2
and \(\quad B=\{x: x \in N and 5<x<6\}\)
Such sets which have atleast one element, are called non-void set.
Note If \(\phi\) represents a null set, then \(\phi\) is never written with in braces i.e. \(\{\phi\}\) is not the null set.
(ii) Singleton Set
A set which have only one element, is called a singleton set.
e.g. A= Set of even prime number
and \(B=\left\{x: x^2 \leq 0, x \in R\right\}\)
(iii) Finite Sets
A set having finite number of elements is called a finite set.
e.g. \(\quad A=\{a, b, c, d\}\)
Here, A is a finite set as it has four elements
(finite number of elements)
(iv) Infinite Sets
A set which does not contain finite number of elements is called infinite set.
e.g. A set of all prime numbers \(=\{2,3,5,7,11,13, \ldots\}\)
Here, A has not finite number of elements, hence it is an infinite set.
(v) Equivalent Sets
Two finite sets A and B are said to be equivalent, if they have the same number of elements.
e.g. If \(A=\{1,2,3\} and B=\{3,7,9\}\)
Number of elements in A=3
and number of elements in B=3
\(\therefore A\) and \(B\) are equivalent sets.


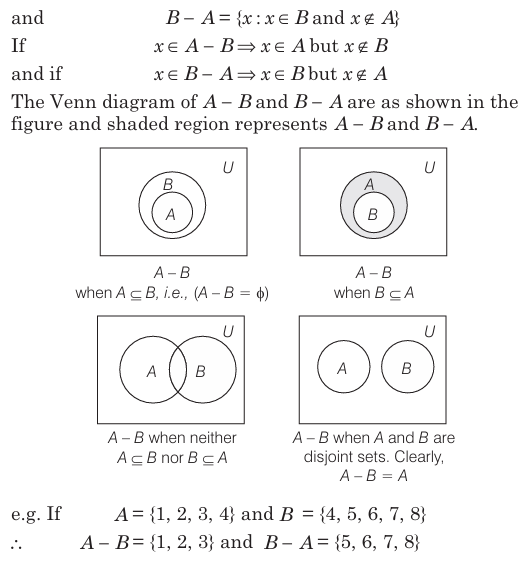
Subset And Superset
Let A and B be two non-empty sets. If each element of set A is an element of set B, then set A is known as subset of set B. If set A is a subset of set B, then set B is called the superset of A.
Also, if A is a subset of B, then it is denoted as \(A \subseteq B\) and read as ' A is a subset of B '.
Thus, if\( x \in A \Rightarrow x \in B, then A \subseteq B\)
If \(x \in A \Rightarrow x \notin B\), then \(A \nsubseteq B\)
and read as ' A is not a subset of B.'
e.g. If \(A=\{1,2,3\} and B=\{1,2,3,4,5\}\)
Here, each element of A is an element of B. Thus, \(A \subseteq B\) i.e. A is a subset of B and B is a superset of A.
Note
- Null set is a subset of each set.
- Each set is a subset of itself.
- If A has n elements, then number of subsets of set A is \(2^n\)
Proper Subset
If each element of A is in set B but set B has atleast one element which is not in A, then set A is known as proper subset of set B. If A is a proper subset of B, then it is written as ' \(A \subset B\) ' and read as A is a proper subset of B.
e.g. If \(N=\{1,2,3,4, \ldots\}\)
and \(\quad I=\{\ldots,-3,-2,-1,0,1,2,3, \ldots\}\)
then\( \quad N \subset I\)
If A has n elements, then number of proper subsets is \( 2^n-1\)


 beeTokens
beeTokens